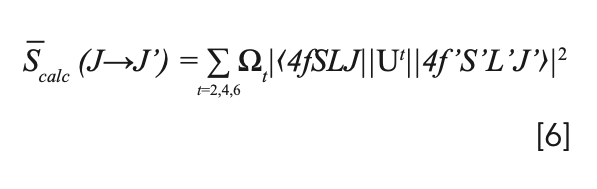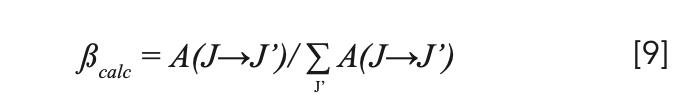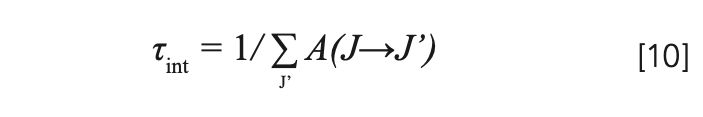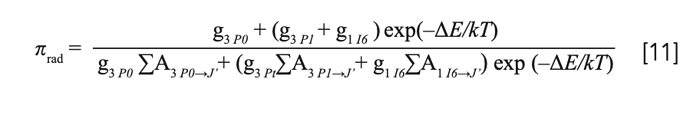Above: YouTube Video. Below, article from Niklas Hammerstone’s web page. Nik, if you find this forum, please join with us.
The following cut and paste from: Diode pumped Pr:Ylf-Laser emitting at 640, 607 and 523nm. — Sci-Projects: Science and engineering at home!
Diode pumped Pr:Ylf-Laser emitting at 640, 607 and 523nm.
Only a few known laser materials are able to emit visible laserlight from visible pump light. One of those materials is the praseodymium ion (Pr3+), which is often doped into Yttrium-Lithium-Fluoride (Ylf) crystals. But Pr:Ylf is not only interesting due to this property. In the following article, I’ll walk you through what makes Pr:Ylf even more special and how one can use this material to make diode pumped solid state (DPSS) lasers emitting at different visible wavelengths with the exact same crystal.
Properties of Pr:Ylf
In order to understand the optical properties important for laser design, we need to look at its absorption and emission spectrum.
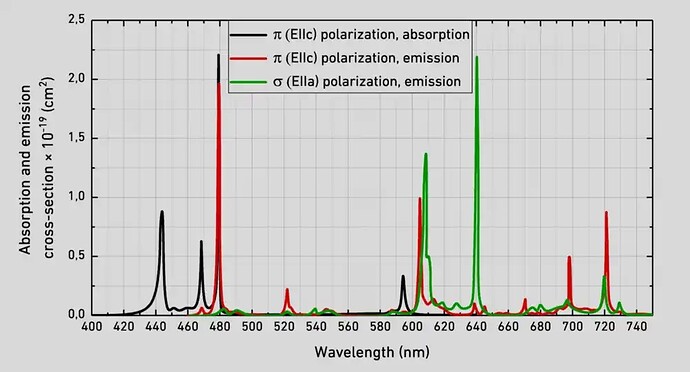
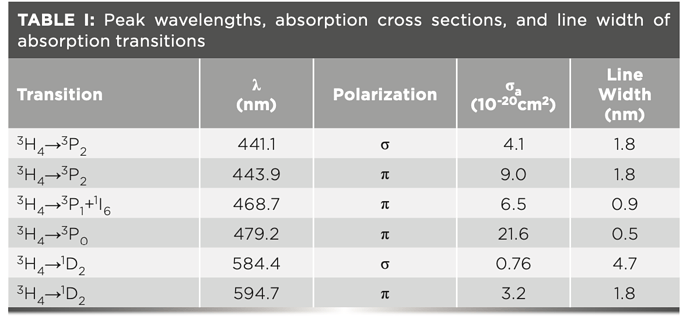
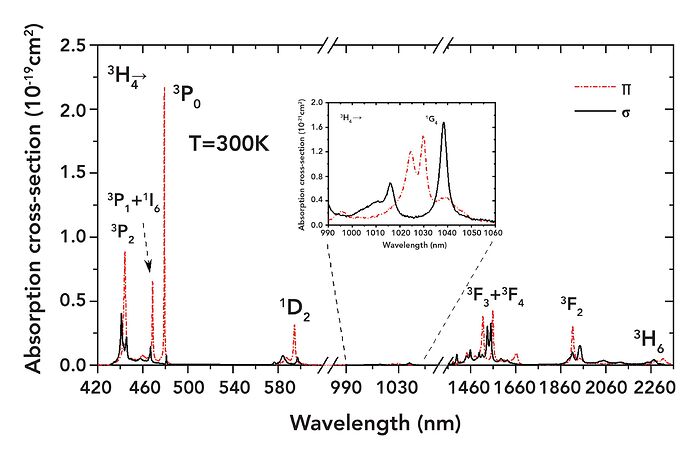
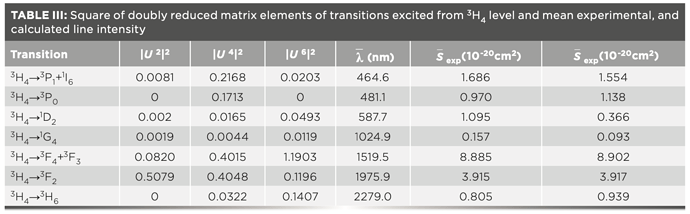
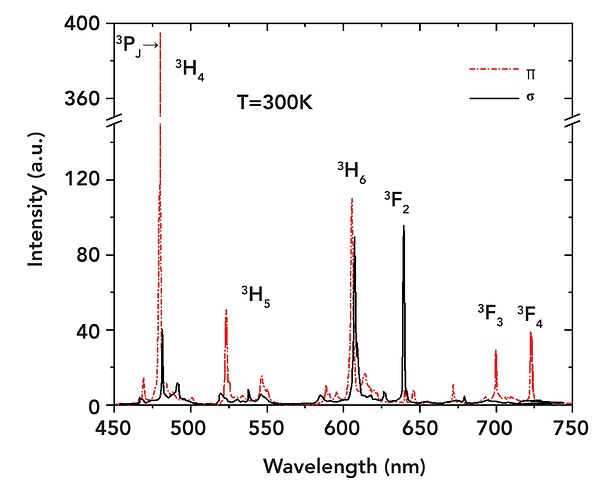
Absorption and emission spectrum of a-cut Pr:Ylf with doping concentration of 1 at.% [[OPTOGAMA]]
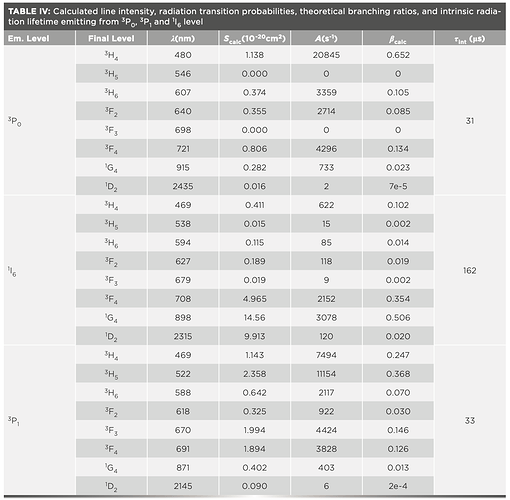
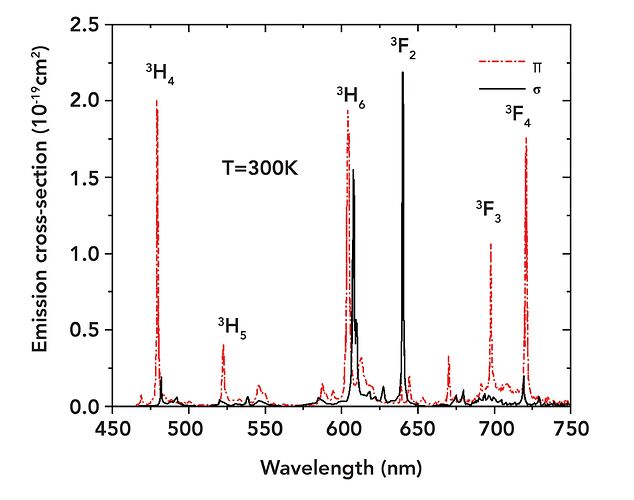
First of all, you can see that there is a very strong absorption peak at 444nm. Therefore, a pump source of this wavelength would be relatively efficient. This is great, because there exist 445nm laser diodes with several watts of optical powers available at very reasonable prices (see chapter Laser design). It is also apparent that Pr:Ylf has a lot of strong emission peaks, depending on polarization. So, not only can it be pumped with visible light and emit visible laserlight, but it can also support a multitude of lasing wavelengths! For example, high emission emission cross-sections at 607nm and 640nm promise high output powers at these wavelengths. There are also notable peaks at 480nm, 523nm, 692nm and 720nm, of which only the peak at 523nm will be of interest in this article. It is obvious that the peak at 523nm has a much smaller amplitude compared to the two peaks mentioned above, so we would expect less output power at this wavelength.
Lastly, we can see that the properties are polarization dependent, so we will have to keep the relative alignment (“roll”) of the pump and the crystal in mind.
Laser design
Going from these properties, we now need to design the pumping source and the laser resonator. Lets start with the resonator, since the pumping source depends on how the resonator is set up.
The resonator
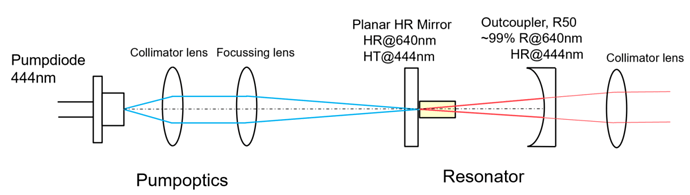
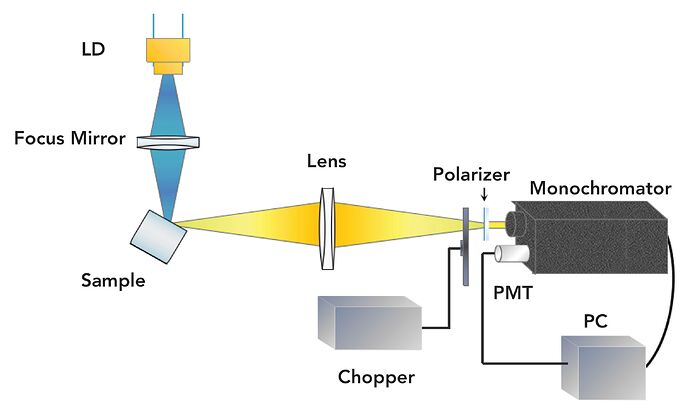
The resonator is the core of any laser. It allows the photons to pass through the excited laser material multiple times, getting amplified each time. There are multiple ways to combine plane, concave and even convex mirrors with each other to make different resonator types with different properties. In this case I chose a hemispheric resonator, which means it consists of one plane (HR, high reflectivity) and one concave (OC, output coupler) mirror. This resonator type is optically quite stable and allows for slight misalignments in the HR mirror without losing resonance. In this article about a DPSS ruby laser I already described this in detail. In order to get sufficient feedback in the resonator, the reflectivities of the mirrors need to be quite high. For the output coupler for the 640nm line (I’ll talk about the other wavelengths further down the article), a reflectivity of about 99% @640nm is used. Transmission values of about 1% for the OC are quite common in the world of continuous wave DPSS lasers. The HR needs to be as reflective for the laser wavelength as possible. Since the crystal I used (2x2x6mm, 0.8% doping), is only polished at the longitudinal faces, the only reasonable pumping method is end-pumping: The pumplight will be focussed into the crystal through the plane HR mirror and excite the laser medium this way. Therefore, the HR mirror must also be quite transparent to the pumping wavelength, in this case 444nm. Both of the mirrors must be mounted in adjustable kinematic mirror mounts. The alignment of the crystal is not as critical since its faces are very parallel to each other, so it will be fixed to a simple metal mount.
The pumping sourcing
Since 445nm laser diodes with high output power exist widely available, choosing one of them is a rather obvious decision. But: since the gain bandwidth of the medium is only a very few nanometers, you’d be lucky if your diode emitted exactly the 444nm that Pr:Ylf needs. Remember that those 445nm diodes usually come with pretty large manufacturing tolerances regarding the output wavelength and also suffer from wavelength shift at different temperatures and currents. To eliminate this uncertainty, I bought a wavelength-selected diode (Type NDB7875) that is guaranteed to emit at 444nm under the specified operating temperature and current. The output beam of the diode is highly divergent and therefore must be collimated before it is focussed into the crystal. I used a combination of an aspheric collimating lens (f=4.6mm) and a biconvex focussing lens (f=50mm). The setup is visualized in the picture below. Note that I also used an edge filter behind the final collimating lens in order to get rid of any transmitted pump light. The resonator length is about 50mm.
The pumping module has quite a lot engineering constraints attached: It must
- securely house the optical components,
- be able to (in this case) watercool the diode to prevent overheating,
- have an attachment point for a temperature sensor,
- be able to be mount into an adjustable kinematic holder,
- be free to rotate, in order to adjust the relativ “roll” of the pump polarisation and the crystal.
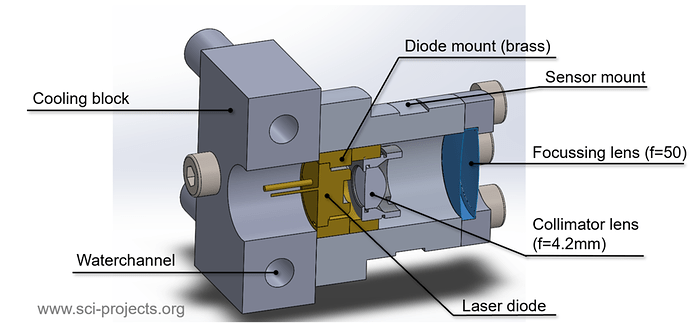
The final design which solved those constraints can be seen in the pictures below.
Sectional view of the CAD Model
Picture of the finished module made from aluminium and brass parts
This design allow watercooling through waterchannels in the cooling block. This is attached to the main housing pieces in which the laser diode is seated. This very compact design also has flat milled sections which allow the attachment of a TO-92 style temperature sensor.
Design implementation
Let us now look at how I put the aforementioned puzzle pieces together. The optical train was realised by mounting the adjustable kinematic holders onto shaft holder trusses (see picture below).
Shaft holder truss by [Dold Mechatronik]
Due to the precise machining of these components, they can be mounted onto two precision rods with little to no play. With a little bit of light oil they move freely along one common axis but can also be clamped very tightly once the alignment is correct.
Since one of the main goals for this project was to make a easy to use laser module which would remain functional even after years of being stored in a dusty basement, I mounted the components onto a sturdy aluminium base plate and bent an alumium sheet as a dust cover. This, by the way, is also the reason why air cooling was not an option for me: If dust were to settle on the optical interfaces it could get baked onto them by the laserbeam and destroy them. The module (without the dust cover) can be seen in the picture below. The combination of the base plate, the hardened precision rods and the trusses makes the setup very sturdy, I can easily carry the module without worrying about the alignment. The trusses at the end are, of course, bolted to the base plate.
As you can see, I used professional mirror mounts (Edmund Optics) for holding the pump module and the output coupler since their alignment is fairly critical. For holding the HR mirror I used a homemade mirror mount since its alignment is not as critical. The holder for the Pr:Ylf crystal is a machined aluminium block. Since the crystal only needs to be translated along the optical axis, it is fixed onto the holder using a very tiny amount of thermal adhesive.
You can also see, besides the beautiful white glow of the crystal, that the module is packed with electronics, which I’ll briefly describe in the next section.
Electronics
In order to maximize the usability of the module, I used an Arduino Nano which measures the diode current, diode temperature, crystal temperature and calculates pump power from the measured current. This information, along with the system status is displayed on a LCD Screen.
The diode driver is controlled by a potentiometer on the front panel. In the picture above you can also see three switches: The right one switches the power to the module, the left one arms the diode driver and the middle one enables active cooling. Once this is activated, two onboard waterpumps circulate water through the diode module and the holder of the crystal. If one of the temperatures reaches a set limit, peltier elements activate and cool down the water going through the overheating element. In practice though, this rarely happens. Also, active cooling of the crystal did not prove to be necessary at the pump powers (<1.2W) I am using. For a detailled electrical schematic and codes please refer to the project’s GitHub repository.
Mirror alignment
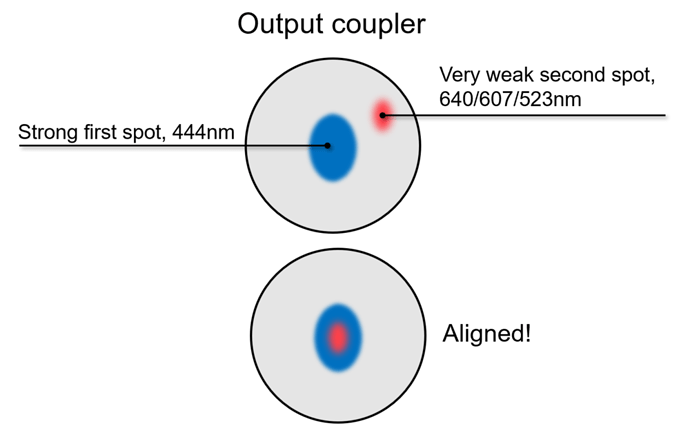
Before we look at the results, lets quickly discuss mirror alignment. This can be quite tricky but if you use the right alignment strategy, it can be done quite effectively. For the ruby laser, looking into the crystal and visually aligning the pump and mode volume worked fine, but since the Pr:Ylf fluoresces much more, it is too bright to see the volumes (even with laser goggles on) once the pump diode thresholds. A much better strategy is to align the cavity by aligning the OC so that the two appearing spots on the output coupler are exactly on top of each other. The first one of the spots is the direct spot of the pumplight. The second spot appears for the following reason (at least I think this is the reason): The pumplight enters the crystal, excites it and creates a weak beam of 640nm photons in the same direction as the pumplight. The beams now hit the OC (this is the first spot) and get reflected into the crystal, where even more coherent photons are created. Since the HR is transmissive for the pumplight, only the 640nm photons get reflected of the HR, pass the crystal once again and hit the OC, creating the second spot. Once the spots are aligned, the beam can resonate back and forth without straying from its path and lasing occurs. This strategy is explained very well in this document by Dr. Walter Luhs. In the picture below, I tried to visualize the strategy as well as I could. Note that the 444nm spot also contains a spot of the laser wavelength, but outshines it by orders of magnitude which is why you can only see the pumplight unless you have got very good goggles. The second spot is very dim, I only was able to see it by switching off the roomlights and very gently blowing on the mirror so that the light condensation (my workshop is quite cold) increased scattering.
Note that for the 607nm mirror, the spots were also visible on the wall behind the mirror which made alignment a lot easier.
Results
The first set of mirrors I used was the mirror set originally intended for the DPSS ruby laser. This allowed the strong 640nm line to get amplified. One short note on this: In this setup, usually only one line gets amplified. As soon as the material is pumped to threshold, the different lines “compete” and the strongest line wins and “takes it all”. Therefore, mirrors for different wavelengths must suppress the stronger lines (e.g. by having low reflectivity for them) in order to get the desired effect. However, this is not necessary if you just want the strongest line to lase, which was the case for the first experiments I did. After aligning the mirrors, the laser produced a very beautiful red output which was quite strong, on the order of 100mW or more, depending on pump power. It also produced some of the most spectacular transverse mode patterns (TEM modes) I have ever seen.
640nm laser action. The intensity inside the resonator is so high that the beam is visible without any smoke in the room. Here, the beam has more or less in a round shape, it operates in a TEM00 mode.
When the mirrors are almost (but not quite) perfectly aligned, the beam is not circular but assumes a more interesting shape, a higher order TEM mode. This is a very clear example of one of those shapes.
This is another example for a very interesting TEM mode. The mode is not fully visible due to the aperture of the output window.
Now, in principle, getting the setup to lase at different wavelengths is just a matter of using a different mirror set. And this worked very well for getting 607nm output, which is orange. I used a concave mirror (R=-100mm) explicitly designed to suppress the 640nm line and the same HR to get the results you can see below. Since the 607nm line is almost as strong as the 640nm one, the output power is very similar.
Apart from some inconsistencies in the beam probably due to imperfect cleaning of the optical elements, the spot is very round. Similarly to the setup above, the intracavity beam is clearly visible.
Here’s a close look at the beam.
Here’s another picture of the setup as a whole. Here you can also see the waterpumps, the arduino and a whole lot of wires.
The wavelength I was really excited about is 523nm. Since the mirror I had for 523nm had virtually no transmission at 523nm, the setup for this wavelength looks a bit different:
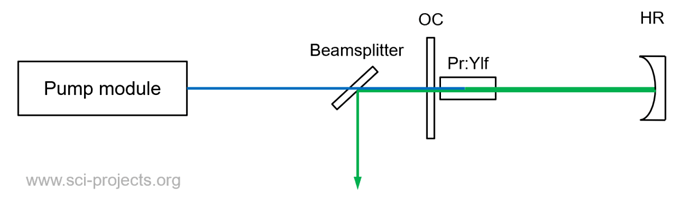
This setup utilizes the fact that the plane HR mirror I had originally bought for 523nm has about 0.5% transmission @523nm and can therefore be used has an output coupler. The concave mirror acts as the HR. Since the laser output now emits into the direction of the pump module, it is selectively reflected using a beamsplitter. Using an edge filter to filter out the few percent of the pumplight yields quite a strong green beam.
Again, the intensity inside the resonator is very high. The additional element in the optical train (referring to the beamsplitter) does make the beam profile a bit inhomogenous, but as you can see, the core “dot” of the output is round.
A beautiful shot of the green intracavity beam emitted from the fiercely fluorescing crystal.
As expected, getting the 523nm line to lase is relatively difficult in comparison to the previous two lines. The alignment is a lot more “fiddly” and the threshold current is pretty high (around 700-800mA). However, looking at the beautiful green output, this has all been worth it.
I can not (yet) provide reliable information on the output power of the module but I will be able to do that very soon. At least for 640nm and 607nm, I am confident that I can exceed 100mW of output power.
So, as you can see, it is possible to utilize this wonderful material, Pr:Ylf, to achieve multiple distinct visible output wavelengths using a relatively simple pumping method. I hope you enjoyed reading this article as much as did making this laser!
Thank you so much for reading,
~Nik